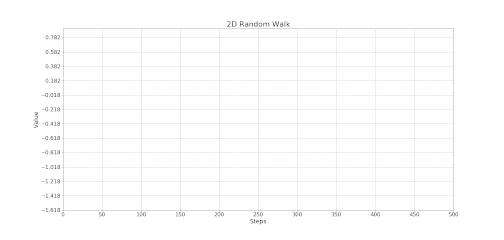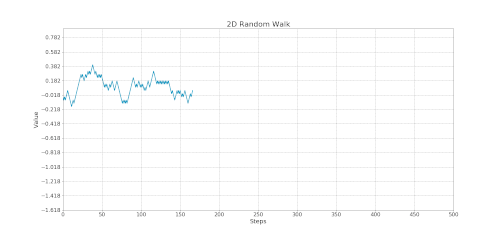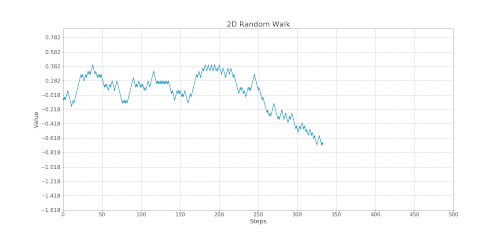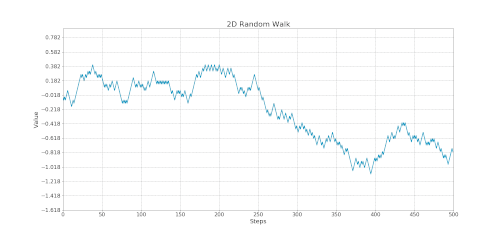
Reflection Principle of Brownian Motion

If the path of a Brownian Motion reaches a value 'a' at time t=s, the reflected Brownian Motion 2a - W(t) from that point and so on, has the exact probability of occurring as the original process. This is known as the Reflection Principle and we can observe it below:

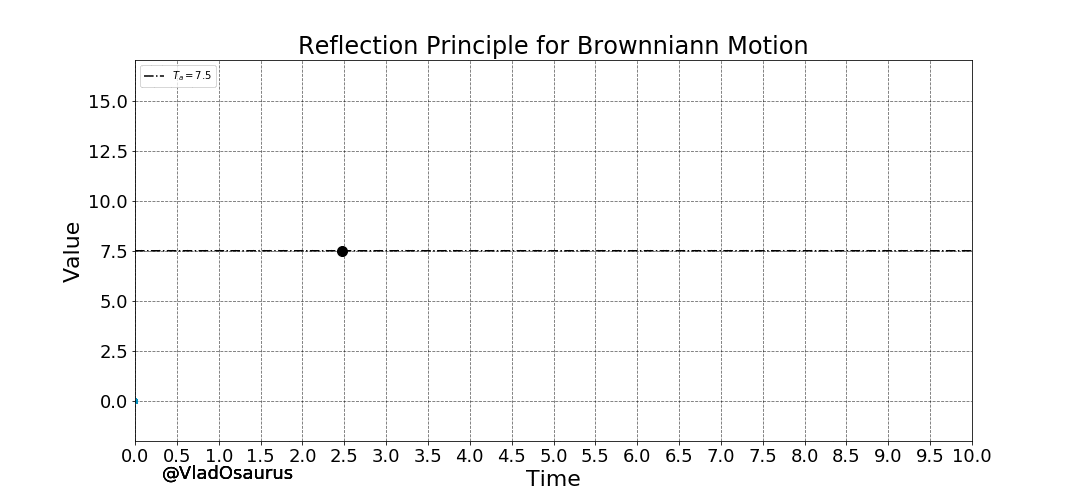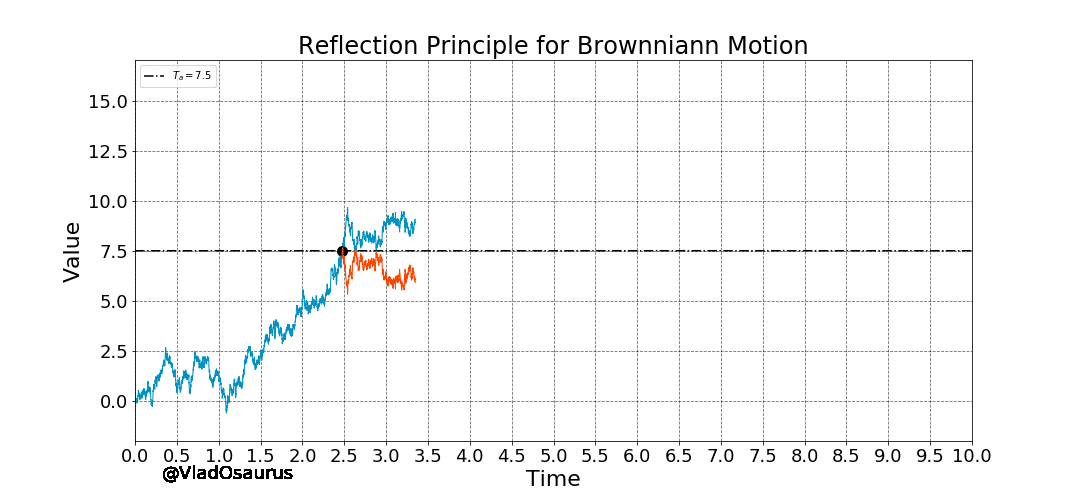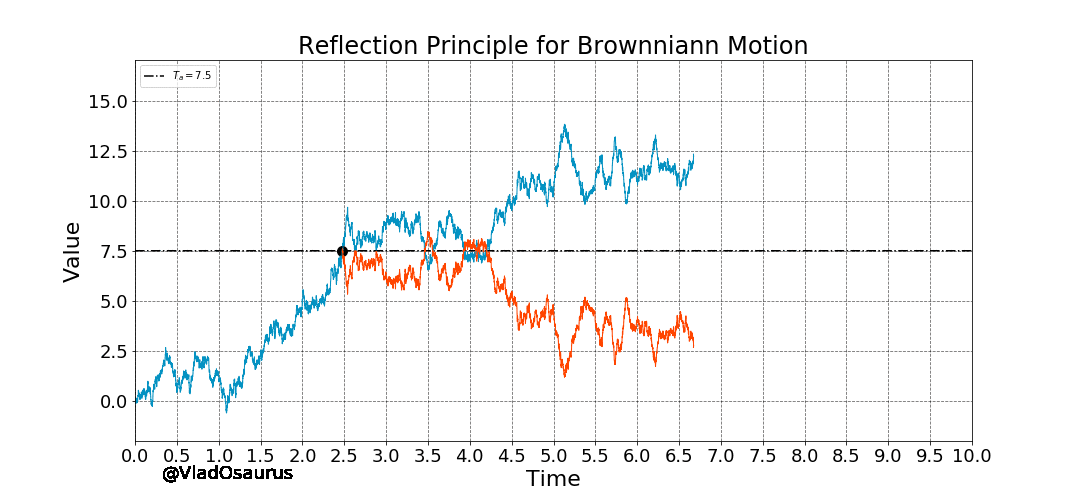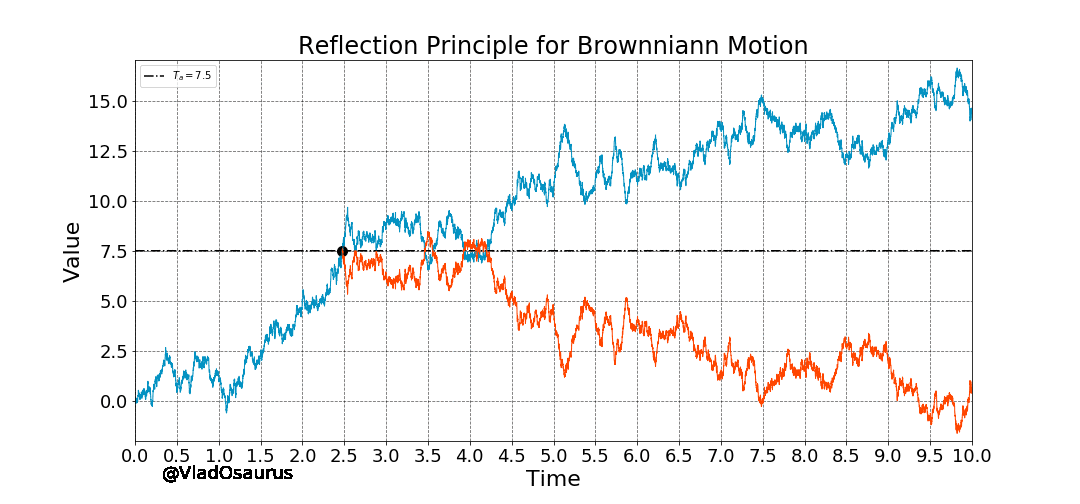
Animation: Reflection Principle of the Brownian Motion

The source code related this visualization can be found in this Jupyter Notebook. For more information, please follow me on Twitter.

If you liked what you just saw, it would be really helpful to subscribe to the mailing list below. You will not get spammed that's a promise! You will get updates for the newest blog posts and visualizations from time to time.